We'll continue to explore functions in this lesson, but now we will look at systems of functions, instead of one function in isolation. This leads to the comparison of different functions as they act upon the same domain. This can be graphically rendered by graphing (f(x),g(x)), where f and g are functions, and x is an element of the domain.
How can we compare two functions? We can think of the graph of a function as picking an element of the domain x, noting the value, f(x), and then plotting (x,f(x)) on the Cartesian plane. Then it would make sense to compare two functions, f and g, by plotting (f(t),g(t)), where t is an element of some domain. This system is called a system of parametric equations, and t is the parameter.
Let's compare cosine and sine. We plot (cos(t), sine(t)) on the Cartesian plane, and see a familiar circle. This should make sense... remember when we discussed the trig functions as relations of the unit circle? Since our hypotenuse was 1, cosine(t) = a/h = x, and sine(t) = o/h = y, and so there should be no surprise that the resulting graph is a circle. We also quickly derive the trigonometric relation cos2(x) + sin2(x) = 1.
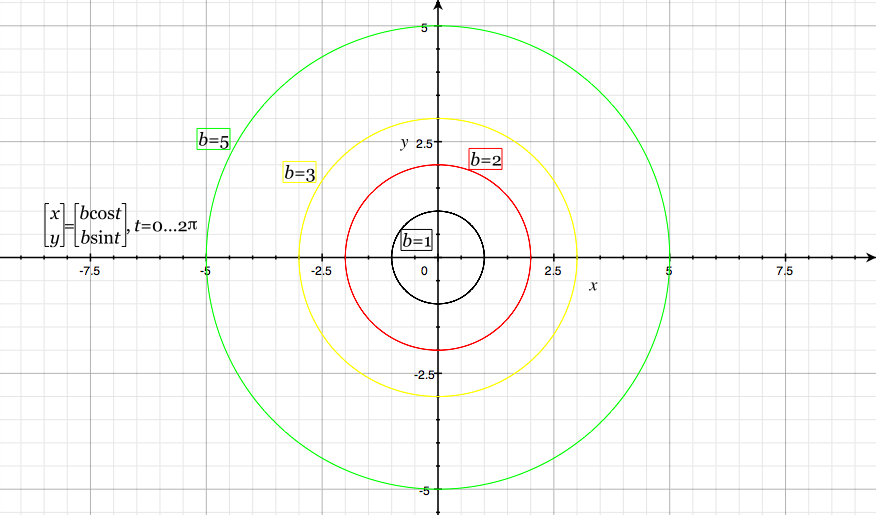
We can investigate the effects of change of parameters, as we did in Assignment 1. For example, let's examine multiplying the expression. For (a*cos(t), b*sin(t)), we are multiplying the base (adjacent to θ) side of the unit triangle by a, and the altitude (opposite to θ) side of the unit triangle by b. In the special case where a = b, then the result is a circle of radius a:

When a and b are different, we can reason that the result will be an elongation along the axis being multiplied.


We can rotate the axes by adding to either argument.

When it comes to multiplying the argument, though, the behavior becomes more dramatic. First, we'll examine the effect on the y = sin b*t parameter:



We notice two things about this. Remember that we are affecting the period of the function. For n*t, the trig function completes the cycle n times. We haven'tchanged the amplitude, so these cycles are completed within a box of +/- 1 along either axis. Look at the case for n=2. The sine function begins at 0, so we start at (1,0). At t = π/4, sin t swoops up to 1, while cos t is about .7 (1,0.7). Then we pass through the origin when cos π/2 = sin π = 0. We can continue in this manner, and locate the critical points on the graph, in other words, points where either x or y are 0, 1, or -1. Connect those points, in order, and we can construct the graph for the curves.
Let's look at cos n*t:



The obvious difference here is that the case for n=2 is not closed. We can examine the critical points as we did for the sine curve. At t = 0, x = 1, y = 0. At t = π/4, x = 0, y = 0.7 (roughly). Then at t = π/2, x = -1, and y = 1. Now here's begins a very subtle and beautiful aspect of trig functions. If you look back at lesson one, sine and cosine are the exact same pattern, but out of phase by π/2. It's easy to be glib about this point while examining their behavior, but here it is a critical difference. Cosine is symmetric about t=0. If you were to observe the behavior of cosine as it moves from t=0, it doesn't matter if you move in the positive or negative direction: cos t = cos -t. Sine, however, is anti-symmetric: sin -t = -sin t. Since we have a point (1,-1) co-incidental on on plot, we have have both functions behaving symmetrically about that point. In other words, they are retracing their steps! Since sin -t = -sin t, we do the same on both sides of the x-axis. When n is odd, we restore the original relationship between the two functions, and the graphs are just π/2 rotations of the sine cases above.
These are just a few examples of a very rich world of relations known as Lissajou graphs.
You may wonder, since we were able to create ellipsoids using trigonometric functions with a common parameter, if we con do something similar to represent hyperboloids. The answer is yes. However, this requires the introduction of the so-called hyperbolic trignometric functions. Our derivation of the ellipsoids using trigs relied upon the relation cos2(x) + sin2(x) = 1, derived from the Pythagorian Theorem. Hyperbolic trig functions, cosh and sinh, rely on the relation cosh2(x) - sinh2(x) = 1. With this relationship defining the hyperbolic trigs, we may construct parametric hyperbolic systems, much the same way as we did with the elliptic trigonometric functions:
